Descubre las dimensiones exactas de un rectángulo dividido en 4 partes

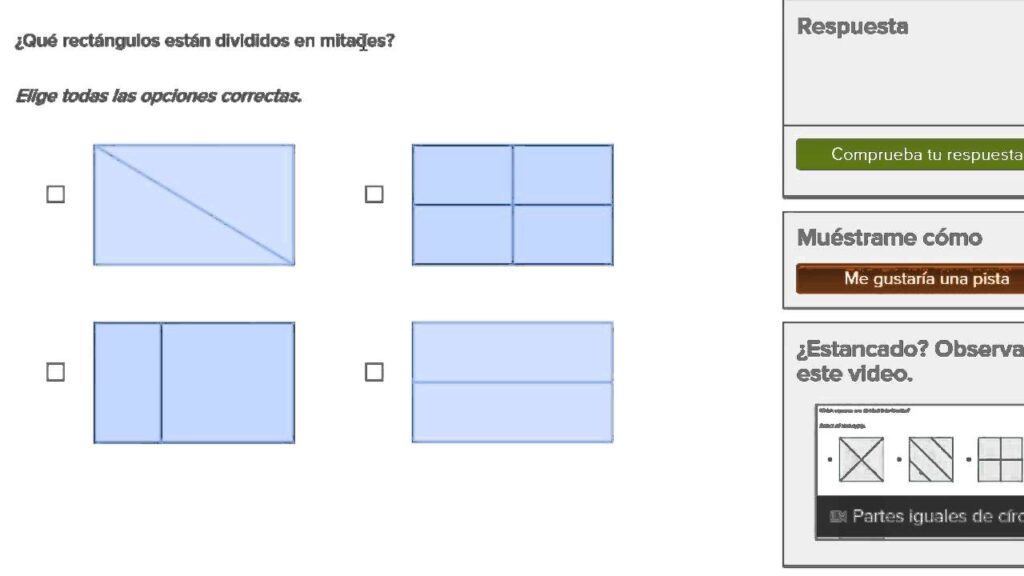
El rectángulo es una figura geométrica de gran importancia en diversas áreas, desde la arquitectura hasta las matemáticas. Conocer las dimensiones de un rectángulo y su división en 4 partes puede resultar muy útil en diferentes aplicaciones. En este artículo, exploraremos la definición de un rectángulo, la importancia de conocer sus dimensiones, así como la forma de realizar su división en 4 partes iguales.

Definición de un rectángulo

Un rectángulo es un polígono de cuatro lados que posee dos pares de lados paralelos y congruentes. Sus ángulos internos miden 90 grados, lo que lo convierte en un cuadrilátero regular. Esta figura geométrica se utiliza ampliamente en diferentes campos debido a sus propiedades y características únicas.

¿Cuáles son las características de un rectángulo?

• Tiene cuatro lados.
• Sus lados opuestos son paralelos y congruentes.
• Los ángulos internos miden 90 grados.
• La suma de los ángulos internos es siempre igual a 360 grados.

¿Cuáles son las fórmulas para calcular el área y el perímetro de un rectángulo?

El área de un rectángulo se calcula multiplicando la longitud de uno de sus lados por la longitud del lado adyacente. La fórmula para el cálculo del área es: Área = base x altura.

Por otro lado, el perímetro de un rectángulo se obtiene sumando todos los lados del rectángulo. La fórmula para el cálculo del perímetro es: Perímetro = 2 x (base + altura).

División de un rectángulo en 4 partes

La división de un rectángulo en 4 partes iguales puede ser útil en diferentes situaciones, como el diseño de espacios, la distribución de elementos o la resolución de problemas matemáticos.

¿Cómo se puede dividir un rectángulo en 4 partes iguales?

Para dividir un rectángulo en 4 partes iguales, se traza una línea horizontal y una línea vertical que se intersectan en el centro del rectángulo, dividiéndolo en cuatro cuadrantes de igual tamaño.

¿Cuáles son las dimensiones de cada una de las partes?

Al dividir un rectángulo en 4 partes iguales, cada parte tendrá la mitad de la base y la mitad de la altura del rectángulo original.

¿Existen otras formas de dividir un rectángulo en 4 partes?

Sí, además de la división en cuatro cuadrantes, es posible dividir un rectángulo en 4 partes mediante líneas diagonales que se intersectan en el centro del rectángulo, formando cuatro triángulos de igual tamaño.

Aplicaciones de la división de un rectángulo en 4 partes

La división de un rectángulo en 4 partes puede ser aplicada en diferentes áreas:

¿En qué áreas se utiliza la división de un rectángulo en 4 partes?

• Arquitectura: para la distribución de espacios.
• Diseño gráfico: para la colocación equilibrada de elementos.
• Matemáticas: en problemas de geometría y proporciones.

¿Cuáles son las ventajas de utilizar esta división en proyectos de diseño?

La división de un rectángulo en 4 partes permite lograr una distribución equilibrada de los elementos en un espacio, brindando armonía y orden visual.

¿Cómo se puede aplicar esta división en el campo de las matemáticas?

En el campo de las matemáticas, la división de un rectángulo en 4 partes puede ser utilizada para resolver problemas de proporciones y relaciones entre áreas.

Cálculos y ejemplos prácticos

¿Cómo se pueden calcular las dimensiones de cada parte en base a las dimensiones totales del rectángulo?

Para calcular las dimensiones de cada parte al dividir un rectángulo en 4 partes iguales, se divide la base y la altura del rectángulo entre 2. Esto nos da las medidas de cada parte.

¿Cuáles son los pasos a seguir para obtener los valores exactos?

1. Obtener la longitud de la base del rectángulo.
2. Obtener la longitud de la altura del rectángulo.
3. Dividir ambos valores entre 2.

¿Puedes proporcionar ejemplos numéricos para ilustrar el cálculo?

Por supuesto, supongamos que tenemos un rectángulo con base de 8 unidades y altura de 6 unidades. Al dividirlo en 4 partes iguales, cada parte tendría una base y altura de 4 unidades.

Consejos y recomendaciones

¿Qué aspectos se deben tener en cuenta al realizar la división de un rectángulo en 4 partes?

Al realizar la división de un rectángulo en 4 partes, es importante asegurarse de que las líneas de división sean rectas y que se intersecten en el centro del rectángulo.

¿Cuál es la importancia de la precisión en las medidas?

La precisión en las medidas es fundamental para obtener resultados exactos al dividir un rectángulo en 4 partes iguales. Pequeñas variaciones pueden afectar la distribución y la armonía visual.

¿Existe alguna herramienta o software que facilite este cálculo?

Sí, existen herramientas y software de diseño que permiten realizar la división de un rectángulo en 4 partes de forma automática, facilitando el proceso y garantizando resultados precisos.

Errores comunes y cómo evitarlos

¿Cuáles son los errores más comunes al realizar la división de un rectángulo en 4 partes?

Al realizar la división de un rectángulo en 4 partes, los errores más comunes suelen ser relacionados con la falta de precisión en las medidas y la incorrecta ubicación de las líneas de división.

¿Cómo se pueden evitar estos errores?

Para evitar errores al dividir un rectángulo en 4 partes, es recomendable utilizar herramientas de medición precisas y realizar trazos cuidadosos. También es importante verificar que las líneas de división sean perpendiculares y que se intersecten en el centro del rectángulo.

¿Cuáles son las consecuencias de cometer estos errores?

Cometer errores al dividir un rectángulo en 4 partes puede resultar en una distribución desequilibrada de los elementos, generando una sensación de desorden y falta de armonía visual.

Conclusiones

La división de un rectángulo en 4 partes iguales es una técnica que puede resultar muy útil en diferentes aplicaciones, desde el diseño de espacios hasta la resolución de problemas matemáticos. Conocer las dimensiones exactas de cada parte garantiza una distribución equilibrada y armoniosa de los elementos. Es importante seguir los pasos adecuados y evitar errores para obtener resultados precisos y satisfactorios.

Preguntas frecuentes

¿Cuál es la importancia de la división de un rectángulo en 4 partes?

La división de un rectángulo en 4 partes permite lograr una distribución equilibrada de los elementos en un espacio, brindando armonía y orden visual.

¿Es posible obtener medidas exactas en la división de un rectángulo en 4 partes?

Sí, es posible obtener medidas exactas al dividir un rectángulo en 4 partes siguiendo los pasos adecuados y utilizando herramientas precisas.

¿Puedo utilizar esta técnica en otros polígonos además de los rectángulos?

Esta técnica específica aplica solo a rectángulos, pero existen otras formas de dividir otros polígonos en partes iguales dependiendo de su forma y características.

¿Existe alguna fórmula general para calcular las dimensiones de la división de un rectángulo en 4 partes?

No existe una fórmula general para la división de un rectángulo en 4 partes, ya que las dimensiones exactas dependen del tamaño original del rectángulo.

¿Cuáles son las principales aplicaciones prácticas de esta división?

La división de un rectángulo en 4 partes puede ser aplicada en diversas áreas, como el diseño de espacios, la distribución de elementos, la resolución de problemas matemáticos y el diseño gráfico.